Someone who tweets under the handle @enn_nafnlaus cautioned that it is easy to make a mistake when comparing trajectories with different exponential growth rates.

In fact, this mistake can bias down the measure of severity that is raising hopes that an omicron infection will be less serious. The bias can be large, off by something closer to a factor of 10 than a factor of 2.

The underlying problem is that fast growth dramatically increases the ratio of any quantity that we measure today compared to its value only a few days ago.

Specific Values

Suppose that omicron is growing at an exponential rate of 20% per day and that we are comparing it to a previous wave where infections were growing half as fast, at the rate of 10% per day. Suppose also that death, if it comes, is on average 3 weeks after the initial infection.

Even if the fraction of infections that end in death is exactly the same for the variants behind the two waves, the ratio of deaths today to infections today will be only one-eighth as large for the omicron wave.

The Graphical Explanation

The simplest way to see where this difference comes from is to use a graph. This one shows the number of infections in a wave using a solid line, and the number of infections 3 weeks earlier using a dashed line.

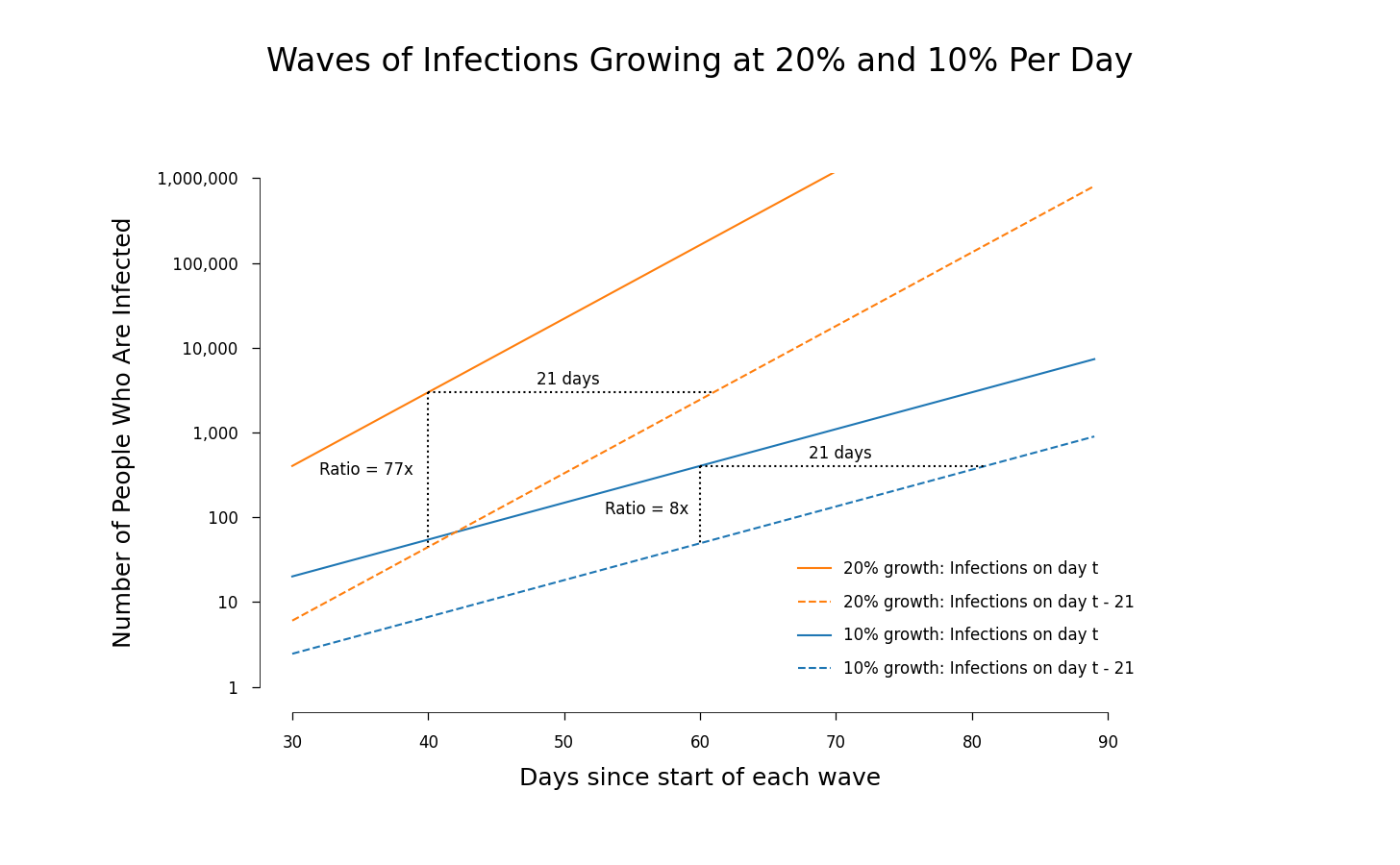
The orange lines are for the omicron wave; the blue for the previous wave. In a graph like this with a ratio (or logarithmic) scale on the vertical axis, exponential growth shows up as a straight line with a slope equal to the rate of growth. For the value on day t, each solid line shows the number of infections on that day of a wave. The dashed line shows the number of infections three weeks before, on day ||t-21||. Each dashed line has the same slope as its solid line one but is shifted to the right by 21 days.

When the slope is steeper, the same horizontal distance implies a bigger vertical distance. The dotted vertical line between two orange curves shows that the number of infections on day ||t|| is 67 times larger than the number of cases on day ||t-21||. The corresponding shorter dotted vertical line between the two blue curves shows that the number of cases on day ||t|| was about 8 times the number of cases on day ||t-21||.

If the same fraction of infections ends in death during these two waves, the number of deaths on day ||t|| is proportional to infections on day ||t-21||. So for omicron, deaths on day ||t|| divided by infections on day ||t|| will be smaller by a factor of $$67/8 \approx 8.$$ It is smaller by this factor because omicron is growing faster.

Moreover, this ||8-||fold difference in the ratio of infections to deaths need not be something that goes away in a few days. It will persist for as long as the period of exponential growth of omicron lasts. This ratio will start to increase only as growth declines to zero and will approach the true infection-fatality rate after the number of infections per day has stabilized at some roughly constant level.

So the ratio of deaths to infections becomes a reliable indicator of severity only after it is too late to use the information it reveals.

Once More, With Math

If you are comfortable with math, there is a simple way to calculate the two numbers cited above. Let ||I^\omicron(t)|| be the number of infections on day ||t|| of the omicron wave and let ||I^\delta(t)|| be the number of cases on day ||t|| of the prior wave. Because omicron is growing at the rate of ||20%|| per day, the ratio ||r|| of current to lagged infections is

$$r^{\omicron} = \frac{exp(0.2t)}{exp(0.2(t-21))} = exp(4.2) = 66.7$$

The corresponding expression for the last wave is

$$r^{\delta} = \frac{exp(0.1t)}{exp(0.1(t-21))} = exp(2.1) = 8.2$$

The Actual Growth Rates

Trevor Bedford reports that his estimate of the doubling time for omicron is 2.3 days in the UK and 3.3 days in Germany. These imply an exponential growth rate of ||30\%|| in the UK and ||21\%|| in Germany so the ||20\%|| growth rate for omicron used in the calculations here is if anything, an underestimate. Using different methods, Tom Wenseleers reports that in South Africa, Belgium, Scotland, Denmark and the UK the exponential rate of growth for omicron is ||30|| percentage points higher than the rate for delta, a difference that is three times the size of the ||10|| percentage point difference used for the calculations here.

Conclusion

As data about the ratio of deaths to infections (or cases) start to trickle in, it would be reasonable to dismiss any modestly smaller value for this ratio as exactly what we would expect when growth is so fast and there is no difference in severity. This type of ratio would have to be smaller by more than an order of magnitude to offer even a hint of a reduction in severity.