In a previous post I described the evidence that pointed me toward the two big questions that guided me when I was building models of growth:

1. Why has the rate of growth been speeding up over time?
2. Why have so many poor countries failed to take advantage of the potential for rapid catch-up growth?

A sign of a good mathematical model is that once you understand it, you can state the answer it suggests very simply. These answers are the final output from the modeling exercise. The models are intermediate inputs.

Here I’ll summarize where things stand on the answer to the first question. In the next post, I’ll do the same for the second question.

Malthusian Rivalry

The way in is to understand scale effects. What possible good can come from having more people around?

In particular, how does output per capita change when there are more people in an economy? The simple point that goes back to Malthus is that if ||R|| is the stock of any rival resource, and ||N|| is the number of people, the per capita stock or resources, ||R/N||, falls with ||N||. Unless there is some offsetting effect, this means that the individual standard of living has to decrease when the number of people increases. To get the pattern we see in the data with a growing population and growing income per capita, something else has to increase in per capita terms when ||N|| increases.

To isolate what that something else might be, consider a thought experiment in which we remove walls that separate people on an island. In the beginning, Alice and Bob live in identical but isolated slices of the island. Each has the same quantity of copper ore, tin ore, iron ore, etc. They also have identical human capital, measured in muscle power. (I trust we can agree that muscles are rival goods.)

Human Capital Can’t Offset Malthusian Rivalry

If we remove the wall, they still have the same quantity of resources per capita. They still have available the same quantity of muscle power per capita, which we can measure in horsepower. An economic theorist can claim that there are “increasing returns to human capital” and assert that when two people who each can produce 0.1 horsepower when they are far apart suddenly can produce 0.3 horsepower when they are close to each other. The theorist can sprinkle “as if” all over these claims, and use words like “agglomeration effects,” but it will still be obvious that the theorist is just making stuff up. There are no scale effects and no external effects associated with human capital qua muscles.

Nothing about this story changes if we admit that a person can invest in more muscle power. Accumulating human capital does not justify scale effects. Human capital is a rival good and there are no scale effects associated with rival goods.

If you have been following these posts, you know what is coming next. Muscle fibers are just like connections in neurons. (If you haven’t been following them, see here.) Human capital can be accumulated in muscle fibers or in neurons. Either way, there are still no scale effects from human capital. (Notice that this claim is logically independent of my claim that human capital is also fully excludable, i.e. that there are no human capital externalities or spillovers. Rivalry and excludability are distinct concepts.)

Nonrival Goods

Next, suppose we allow for the existence of some nonrival goods, such as some recipes for rearranging natural resources. Suppose in particular, that through a long process of trial and error, Alice has discovered the recipe for mixing copper with tin to make the more valuable metal bronze. And in the same way, Bob has spent many hours discovering and refining a recipe for mixing iron with carbon to make steel.

After the wall is removed, if Alice and Bob can communicate what they know to each other, then they have the same quantity of natural resources per capita and same amount of muscle power per capita, but they have twice as many useful recipes per capita. They can both have both of the recipes.

It is the presence of nonrival goods that creates scale effects. Using the jargon of mathematical economics, this is because nonrival goods introduce a “nonconvexity” into production possibilities. And to follow up on one deferred issue from a previous post, this nonconvexity from a nonrival good will be present and will create scale effects associated with increases in ||N|| even if it is costly to communicate with each other. All that is required is that the cost of learning a recipe from someone else is less than the cost of discovering it independently. Suppose it takes 1,000 hours of person effort to find each recipe and it takes 3 hours of conversation between Alice and Bob to communicate one recipe, which means a total of 6 person hours to communicate it. Think of the productive resource as a brain that has a recipe stored in its neurons.

With these assumptions, it takes 1,000 hours of person effort to produce the first instance of a brain with neurons that hold the instructions for making bronze, but only 6 additional person hours to produce the second brain holding instructions for making bronze. This kind of “falling cost,” or this high “first copy cost” followed by low costs for additional copies is the source of the scale effects. As long as communication takes less than 1,000 hours of person effort, recipes are nonrival goods and they generate scale effects.

Undiscovered Nonrival Goods Yield Scale Effects

Once we assume that

(i) there exist nonrival goods such as recipes that people can communicate with each other, and

(ii) that there are many valuable nonrival goods that remain to be discovered,

there is a benefit to being around other people. This point is easiest to see if we treat the copying or communicating costs as being negligible. Then if ||A|| represents the stock of ideas it is also the per capita stock of ideas. Bigger ||N|| means bigger ||A|| so bigger ||N|| means more ||A|| per capita. It is still true that per capita stock of resources ||R|| goes down with ||N||. From the point of view of the individual, having more people around now has both a benefit and a cost and it is logically possible that benefits from more recipes per capita will outweigh the costs of fewer resources per capita. At least in the activity that Malthus (and Paul Ehrlich) worried about, the evidence shows that with a falling quantity of surface area on the earth per capita, better recipes have nevertheless allowed an allowed an increase the annual production of food per capita.

Note that in this argument, assumption (ii) is important. If there is a fixed set of useful nonrival recipes but we already know all of them, then we can share the ones we have but having more people around will not give us any more. This is why the key to understanding growth to combine two distinct concepts: nonrival goods and the process of combinatorial explosion that I discussed in a previous post.  We are lucky to in a physical world characterized by combinatorial explosion and to be creatures with an evolved capacity for communicating with each other.

Explaining Why Growth Speeds Up

So nonrival goods and combinatorial explosion explain why increases in standards of living are possible. What does it take to explain why the standard of living has been increasing at a pace that has increased from one century to the next?

a) The idea that I considered in my 1983 Ph.D. thesis was in effect that as the stock of ||A|| increases, it becomes even easier to discover new ideas. Machine learning might be an example of this. You discover some ideas that then make it easier to discover lots more. The more you know, the easier it is to discover more. (At that point, I still did not understand the importance of nonrival goods and did not rely on scale effects.)

b) The scale effects showed up in a paper by the demographer Ron Lee in 1988 and independently in my 1990 paper. As there are more people, they produce more ideas. Ron closed the loop by observing that with more ideas (particularly about how to raise food), you can also get more people, so he generated a simple model of accelerating growth in population illustrated in Figure 1 (from Jones and Romer, 2010. Also, see this paper for the cite to Lee’s paper.)

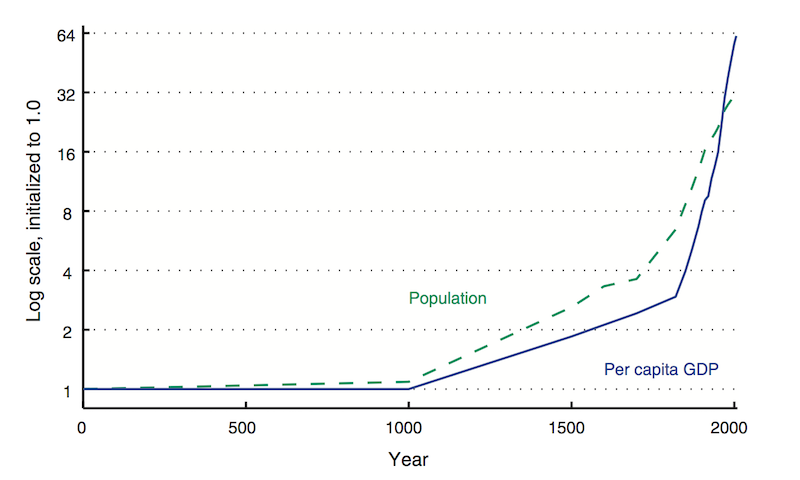Figure 1

If we layer in some reason why fertility does not keep up with a rapidly growing supply of food, then you can also get the second one curve to, with a lag, accelerating growth in income per capita. Then as total population stops growing as rapidly, the supply of human capital ||H|| measured for example in total years of education in the workforce can grow as educational attainment grows. This was the scale effect in my 1990 model. It is captured in Figure 2, which is taken from the paper. It shows how the stock of human capital ||H_A||, which is devoted to discovery, increases with the the total stock of ||H||. Because I assumed that the rate of growth was proportional to the quantity ||H_A|| of human capital allocated to discovery, growth increases in the same way.

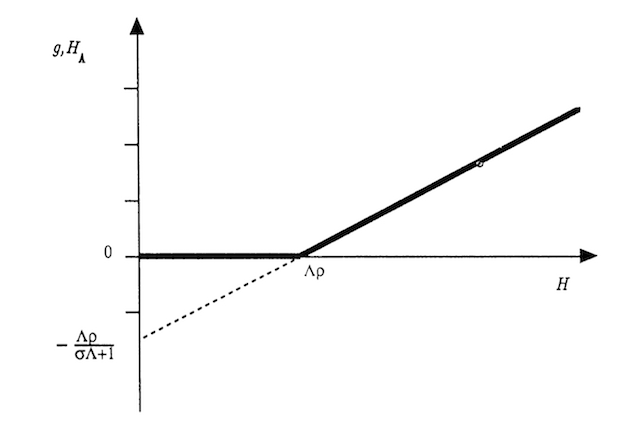Figure 2

Chad Jones then argued convincingly that given how fast total ||H|| has grown, there has to be a type of fishing out effect that was making it harder to find good ideas as time progressed. So in the Jones elaboration, growth speeds up entirely because of the scale effect. In his model, the more you know, the harder it is to discover new things because the pond of knowledge is getting “fished out.”

As we show in our joint 2010 paper, although the implications of his model and my model 1990 are different when you take the limit as time ||t|| goes to ||\infty||, they are similar over time spans on the order of a century. In particular, they offer the same optimism about the potential for better policy to yield faster growth for several generations.

c) Recently, I’ve been thinking about a restricted version of the idea from my thesis that “the more you know, the easier it is to …” do something. But now, that something is communicate and this interacts with the scale effects. As ||N|| grows, it is valuable to reduce even small communication costs. If people are spread over geographic space, one of the costs is the time it takes to travel. For example, estimates suggest that wheat spread from the Fertile Crescent to Europe at the rate of about 1 km per year. Even if there are a lot of people spread over the surface of the earth, if ideas move at walking speed, the scale effects on growth will be limited.

One solution humans found for facilitating communication was to collect a lot of people together who all live within walking distance of each other–by inventing the city. (As I pointed out here, the city was not just a good idea. It was a meta-idea, an idea about how to produce lots of ideas.)

In parallel, we also discovered some meta-ideas that enhance the rate of communication across large distances and over time–written language, printing, and digital communication. Like cities, these are meta-ideas, ideas about how to produce and distribute ideas. They interact with population size to enhance the scale effects and convert them from local effects into global effects.

It would be better to describe this as “the more you know, the better it is to have lots of other people around, not just nearby, but anywhere on earth.”

---

Previous posts in this series:

#5: Speeding Up and Missed Opportunities: Evidence

#4: Economic Growth

#3: Clear Writing Produces Clearer Thoughts

#2: Human Capital and Knowledge

#1: Nonrival Goods After 25 Years

Thanks to Joshua Gans for spurring this series with his post here.